 Transformation matrix
Transformation matrix
Bilbao Crystallographic Server  Transformation matrix Transformation matrix
|
| P = |  |
|
 |
|||||||||
 | P11 | P12 | P13 |  | |||
| (a', b', c') = (a, b, c)P = (a, b, c) | P21 | P22 | P23 | = | (aP11+bP21+cP31, aP12+bP22+cP32, aP13+bP23+cP33) | ||
| P31 | P32 | P33 |
 | p1 |  | |
| p= | p2 | ||
| p3 |
|
|
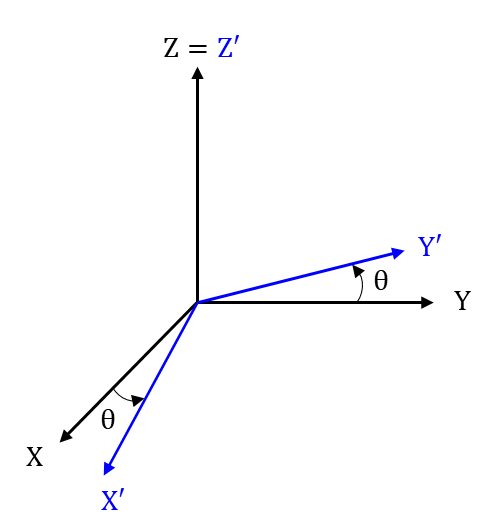 |
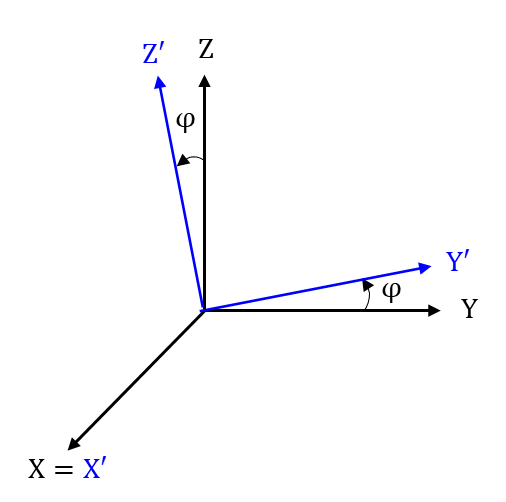 |
 |
| R = |  |
|
 |
 |
|
 |
 |
|
 |
|
Bilbao Crystallographic Server http://www.cryst.ehu.es |
For comments, please mail to administrador.bcs@ehu.eus |